• OPC UA Python Bibliothek
• OpenCV Python Bibliothek
• Pillow Python Bibliothek (inklusive Image Modul)

Um auf dieses Onlinelabor zuzugreifen, benötigen Sie folgende Informationen:

• Namespace-URI: opc.tcp://engine.ie.technikum-wien.at/BallMaze
• Root-Node des Kugellabyrinths: ns=1;s=Ballmaze
• Benutzername: ballmaze

Die Grundlagen der Kommunikation können Sie HIER nachlesen. Beachten Sie bitte, dass eine Interaktion mit der Hardware nur über das Kommunikationsprotokoll OPC UA möglich ist.

Die Steuerung des Kugellabyrinths erfolgt von außen nur durch einen OPC UA Server, welcher die Befehle an ein SPS (Speicherprogrammierbare Steuerung) weiterleitet, um das Kugellabyrinth anzusteuern. Für den Zugriff von Außen wird ein OPC UA Client benötigt. Dieser Client muss verschiedene Knoten, sowie deren Werte vom Server auslesen und beschreiben können. Dies geschieht über Methoden, welche am Server implementiert sind. Jeder Wert besitzt eine eindeutige Identifikationsnummer, mit welcher dieser Wert ausgelesen und beschrieben werden kann. Für die folgende Programmierung wird auf die OPC UA Bibliothek von Python zurückgegriffen.

Als ersten Schritt empfiehlt es sich, den OPC UA Server des Kugellabyrinths etwas genauer zu betrachten. Hierzu wird am besten das Programm UA Expert von Unified Automation verwendet. Dabei handelt es sich um einen OPC UA Client, welcher das Durchsuchen des Namensraumes unterstützt und alle Knoten (engl.: node) und Methoden übersichtlich darstellt. Es ist auch möglich einen Live-Video Stream der Kamera des Kugellabyrinths abzurufen.

Zum eigentlichen Lesen und Schreiben von Werten muss zu Beginn eine Verbindung zum Server aufgebaut werden. Diese Verbindung wird mit Hilfe eines Benutzernamens und eines Passworts authentifiziert. Für die Anmeldung am Server werden in einem Python Script die Funktionen Client() und connect() verwendet. In der Funktion Client() werden Benutzername, Passwort, Hostname sowie Port übergeben, um mit der Funktion connect() die Verbindung herzustellen. Danach kann mit der Funktion get_namespace_index() der Namensraum des Kugellabyrinths ausgewählt werden, um anschließend auf die Knoten zugreifen zu können. Mit der Funktion get_node() ist unter Angabe des Namensraums und der Kennung (engl.: identifier) des entsprechenden Knotens ein Zugriff möglich. Mit der Funktion get_value() ist ein Lesen des im Knoten beinhalteten Wertes möglich. Falls es der OPC UA Server erlaubt können auch Werte eines Knotens direkt mit set_value() geschrieben werden. Normalerweise und um zu gewährleisten, dass nicht unzulässige Werte in einen Knoten geschrieben werden, wird der Schreibvorgang über eine Methode erledigt und sind Werte nicht direkt beschreibbar. Über eine Methode kann der Wert, welcher verändert werden soll, überprüft und bei Unzulässigkeit verworfen werden.

Um eine Methode aufrufen zu können, wird die Funktion call_method() verwendet. Mit dieser Funktion lassen sich sowohl Werte aus der Methode lesen, als auch in diese schreiben, um so das System anzusteuern. Als letzten Schritt ist es unbedingt erforderlich, mit der Funktion disconnect() die Verbindung zum Server wieder zu schließen. Manche OPC UA Server verneinen das Eingehen von mehreren parallelen Verbindungen um Konflikte zu vermeiden. Ist die Verbindung nicht ordnungsgemäß beendet worden, muss diese am Server manuell beendet werden.

Jede Kamera besitzt ein gewisses Maß an Verzerrung und Störung. Das liegt an der Linsenkrümmung und an dem Aufbau einer Kamera. Für exaktes Ausmessen von Längen oder zur genauen Bestimmung einer Position im Kamerabild ist es daher wichtig, die Kamera zuerst zu kalibrieren. In diesem Schritt wird die Kamera entstört und auf ein definiertes Muster kalibriert. Es gibt eine Reihe von verschiedenen Kalibrierverfahren, wobei in dieser Übung mit Hilfe eines Schachbrettmusters gearbeitet wird. Das Ergebnis eines solchen Prozesses ist eine Kameramatrix, welche genau die einzigartige Verzerrung und Störung der verwendeten Kamera beschreibt. Somit ist es dann möglich, exakte Distanzen auch mit nur einer Kamera zu messen.

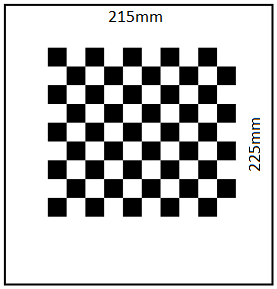
Bei einer Kamerakalibrierung gibt es einige Schritte, welche notwendig sind, um ein entstörtes kalibriertes Bild zu erhalten. Für die Kalibrierung wird ein Schachbrettmuster verwendet, welches zuerst aus verschiedenen Positionen und Orientierungen mit der Kamera fotografiert werden muss. In der folgenden Abbildung wird ein solches Schachbrett gezeigt. Die Dimensionen des Kalibrierobjekts betragen:

• Breite der Umrandung: 215mm
• Höhe der Umrandung: 225mm
• Anzahl der Kacheln: 10x9
• Kachellänge: 15mm

Da das Kugellabyrinth im Normalbetrieb nur über fest montierte Kameras verfügt, werden verschiedene Fotos zur Verfügung gestellt. Diese können HIER heruntergeladen werden. Im ersten Schritt gilt es herauszufinden, welche der Fotos für eine Kalibrierung geeignet oder nicht geeignet sind. Nur Fotos mit ausreichender Belichtung, Schärfe und Kontrast sowie Fotos, welche überhaupt ein Schachbrettmuster der richtigen Dimension enthalten, sind zulässig. Mit der Funktion cv2.findChessboardCorners() kann jedes einzelne Bild auf ein Schachbrettmuster der richtigen Dimension überprüft werden. Wichtig ist hierbei, dass die Funktion nur mit Bildern in Graustufen arbeiten kann. Weiters ist zu erwähnen, dass alle zu überprüfenden Bilder die gleiche Auflösung, das bedeutet auch von der gleichen Kamera, mit denselben Einstellungen stammen sollten. Ist dies nicht der Fall, so wird die Funktion cv2.findChessboardCorners() nicht korrekt ausgeführt. Es ist unbedingt erforderlich, vorher die Bilder auf deren Auflösung zu prüfen. Mit den Funktionen image.get(cv2.CAP_PROP_FRAME_WIDTH) und image.get(cv2.CAP_PROP_FRAME_HEIGHT) ist es möglich die Breite und Höhe jedes eingelesenen Bildes auszulesen. Somit kann jeder Wert abgespeichert und mit Werten anderer Bilder verglichen werden.

Sobald im ersten Schritt Kanten des Schachbretts in einem Bild erkannt wurden, müssen diese in einer Variable abgespeichert werden. Zusätzlich müssen sogenannte Bild- und Objektpunkte definiert werden. Die Bildpunkte (engl.: image-points) geben den Pixelwert der gefundenen Kante des Schachbretts im jeweiligen Bild an. Wenn ein Bild in Python geladen wird, dann liegt dieses als Matrix vor. Die Anzahl der vertikalen Matrix-Einträge entspricht der Höhe des Bildes in Pixel, die Anzahl der Horizontalen der Breite. Somit kann bestimmt werden, wo genau auf dem Bild sich eine Kante des Schachbretts befindet. Die Objektpunkte hingegen beschreiben, wo sich die Kante des Schachbretts in einem dreidimensionalen Koordinatensystem in der Realität befindet. So kann beispielsweise festgelegt werden, welchen Abstand die Kanten zueinander und welche Größe die Kacheln des Schachbretts haben. Somit ist es dann auch weiterführend möglich, die Position von Gegenständen im Raum zu bestimmen.

Sind die Bild- und Objektpunkte deklariert so müssen anschließend zu jedem Bild, in welchem Kanten erkannt wurden auch diese Punkte zugeordnet werden. Der spätere Kalibrierungsprozess ist nur erfolgreich, wenn genügend Bilder mit Bild- und Objektpunkten versehen wurden. Für eine Kalibrierung sollten mindestens zehn valide Bilder verwendet werden. In der Theorie funktioniert eine Kamerakalibrierung mit nur zwei, aus unterschiedlichen Winkeln aufgenommenen, Bildern. Je mehr Bilder allerdings verwendet werden, desto besser funktioniert der Prozess.

Mit der Funktion cv2.cornerSubPix() werden die bestimmten Kanten des Schachbretts in jedem einzelnen Bild noch verfeinert. Diese verbesserte Darstellung der wirklichen Eckpunkte eines Feldes im Schachbrett ist notwendig, um die Genauigkeit der nachfolgenden Kalibrierung zu gewährleisten. Mit den verfeinerten Kanten können nun auch zur Veranschaulichung die einzelnen Punkte grafisch ausgegeben werden.

Der letzte Schritt ist die eigentliche Kamerakalibrierung. Von der Funktion cv2.calibrateCamera() wird schlussendlich eine Kameramatrix und ein Verzerrungskoeffizient zurückgegeben. Diese sollten unbedingt in einer Datei abgespeichert werden, um sie bei den weiteren Übungen wiedereinzusetzen und genaue Ergebnisse zu erhalten.

Um die Kugelposition im Labyrinth zu verfolgen und eine Regelung zu ermöglichen, muss die Position der Kugel detektiert werden. Es gibt einige Methoden, um geschlossene Objekte zu erkennen. In dieser Übung wird mit einer sogenannten Hough Transformation gearbeitet. Diese kann für eine Kreis- und Linienerkennung verwendet werden.

Zu Beginn dieser Aufgabe muss ein Bild in das Programm geladen werden. Mittels Hough Transformation sollen in diesem Bild Kreise detektiert werden. Die Hough Transformation wird allgemein zum Erkennen geometrisch bekannter Formen verwendet. Dazu werden Bilder in den Hough-Raum transformiert. Jeder Punkt, der auf einer Kante (Geraden) liegen könnte, wird zunächst als Schnittpunkt von unendlich vielen Geraden bezeichnet. Im Hough-Raum ist dann für Punkte welche auf einer gemeinsamen Geraden liegen eine Häufung zu sehen. Diese Häufung beschreibt eine Gerade oder Kante im echten Bild. Zu beachten ist, dass der Hough Algorithmus nur mit Bildern in Graustufen arbeiten kann. Um Kreise vernünftig erkennen zu können, ist es notwendig das Bild mit einem Blur Filter zu verändern. Dieser Filter sorgt dafür, dass Kanten des Bildes weichgezeichnet werden und nur Kreise erkannt werden, welche auch wirklich Kreise sind. Mit der Funktion cv2.medianBlur() kann eine solche Wirkung erzielt werden. In der folgenden Abbildung ist ein Symbolfoto zu sehen welches diese Funktion deutlich macht. Es ist anschaulich zu erkennen, dass die Kanten des Symbolbildes weichgezeichnet wurden.

Im nächsten Schritt können mit Hilfe der in OpenCV enthaltenen Funktion cv2.HoughCircles() Kreise detektiert und diese in einer Variable abgespeichert werden. Zum Debuggen der Funktion cv2.circle() ist es hilfreich, wenn die gefundenen Kreise auch grafisch im Bild hinterlegt werden.

Stellen Sie eine Verbindung zum Kugellabyrinth her. Eine Anleitung hierzu finden Sie in der Onlineübung zu OPC UA. Die Zugriffsinformationen sind im Grundlagenteil dieses Labors zu finden.

Es wird empfohlen, zunächst eine Verbindung mittels UA Expert herzustellen und den Aufbau der Serverstruktur zu studieren. Mithilfe dieses Programms können Sie auch bereits Sensorwerte auslesen, den Kamerastream betrachten und die Aktuatoren auf Zielpositionen bewegen. Schreiben Sie anschließend ein einfaches Kommandozeilenprogramm, dass nacheinander alle Aktoren zunächst getrennt von einander und anschließend simultan ansteuert. Geben Sie alle Sensorwerte und das Kamerabild nach jeder Bewegung aus. Sie sehen, wie die Bewegungen die gemessenen Werte beeinflussen (z.B. Rotation um die verschiedenen Achsen des Kugellabyrinths).

Erweitern Sie Ihr Programm aus der ersten Übung so, dass das Kamerabild bzw. die Sensorwerte als stetiger Stream ausgegeben werden. Implementieren Sie eine Steuerung über die Kommandozeile: Durch Drücken verschiedener Tasten auf der Tastatur soll das Kugellabyrinth angesteuert werden (z.B. Neigung um die Achsen steuern mittels Pfeiltasten). Mithilfe dieses Programms sollen Sie das Labyrinth manuell durchfahren können.

Um die Kugel im Labyrinth von einem Programm verfolgen zu lassen, ist im nächsten Schritt eine Kamerakalibrierung notwendig. Eine detaillierte Übungsbeschreibung im PDF-Format zur Durchführung der Kamerakalibrierung kann HIER heruntergeladen werden. Die Übung bezieht sich auf den Puzzlebot, kann aber in der exakt gleichen Vorgehensweise für das Kugellabyrinth durchgeführt werden. Die notwendigen Bilder für die Kamerakalibrierung können HIER heruntergeladen werden.

Implementieren Sie einen Algorithmus, der die Kugelposition aus den Bildern des Kamerastreams ermittelt. Verwenden Sie hierzu die im vorherigen Schritt bestimmte Kameramatrix zum Entstören der Bilder. Zum Detektieren der Kugel gibt es verschiedene Möglichkeiten (z.B. Form, Farbe). Testen Sie verschiedene Verfahren, um die Kugelposition möglichst zuverlässig zu detektieren. Zeigen Sie die Position der Kugel im Bild an, indem Sie einen farbigen Kreis an der Kugelposition anzeigen. Lassen Sie sich außerdem die Koordinaten des Mittelpunkts der Kugel anzeigen.

Um das Kugellabyrinth automatisch durchfahren zu lassen, müssen Sie die in den vorherigen Schritten implementieren Funktionen adaptieren und zusammenführen. Es gibt unzählige Möglichkeiten, die Aufgabe des automatischen Durchfahrens des Labyrinths mittels Regelungstechnik zu lösen. In dieser Übung wird eine relativ einfache Vorgehensweise vorgeschlagen: Programmieren Sie eine State-Machine, die Abhängig von der Position der Kugel die Aktuatoren anspricht, um in den nächsten State zu gelangen. Ihre States werden aufgrund der Kugelposition bestimmt. Beachten Sie, dass diese leicht Schwanken kann, weshalb Sie nicht auf exakte Werte prüfen sollten, sondern einen gewissen Threshold zulassen sollten. Zum Beispiel starten Sie in State_0 (Anfangsposition) und möchten in State_1 gelagen. Sie müssen die Aktuatoren derart ansteuern, dass sich die Labyrinthplatte stark in die eine Richtung, und schwach in die andere Richtung neigt. Sobald die Kugel State_1 erreicht, benötigen Sie Steuerungsbefehle um in State_2 zu gelangen usw. Sie müssen überprüfen, ob der Folgestate auch wirklich erreicht wird und falls nicht weitere Aktionen setzen. Benutzen Sie auch die binären Sensoren des Kugellabyrinths zur Überprüfung der States.
Die Steuerungsbefehle können Sie unter Zuhilfenahme des Programms zum manuellen Durchfahren des Labyrinths ermitteln. Die Positionen für die Definition Ihrer States liefert Ihnen das Programm zur Erkennung der Kugelposition.

Mit dieser Funktion werden Bilder hinsichtlich eines Schachbrettmusters mit bestimmter Dimension überprüft. Dadurch kann festgestellt werden, ob sich die Bilder für eine Kamerakalibrierung eignen.

Sie ermöglicht es, bekannte Geometrien wie z.B. Kreise in Bildern zu erkennen. Die OpenCV Python Bibliothek enhtält bereits Funktionen, um bestimmte Geometrien zu identifizieren. Beispielsweise wird für die Erkennung von Kreisen die Funktion cv2.HoughCircles verwendet.