• OPC UA Python Bibliothek
• OpenCV Python Bibliothek
• Pillow Python Bibliothek (inklusive Image Modul)

Um auf dieses Onlinelabor zuzugreifen, benötigen Sie folgende Informationen:

• Namespace-URI: opc.tcp://engine.ie.technikum-wien.at/PuzzleBot
• Root-Node des Puzzlebot: ns=1;s=Puzzlebot
• Benutzername: puzzlebot

Die Grundlagen der Kommunikation können Sie HIER nachlesen. Beachten Sie bitte, dass eine Interaktion mit der Hardware nur über das Kommunikationsprotokoll OPC UA möglich ist.

Jede Kamera besitzt ein gewisses Maß an Verzerrung und Störung. Das liegt an der Linsenkrümmung und an dem Aufbau einer Kamera. Für exaktes Ausmessen von Längen oder zur genauen Bestimmung einer Position im Kamerabild ist es daher wichtig, die Kamera zuerst zu kalibrieren. In diesem Schritt wird die Kamera entstört und auf ein definiertes Muster kalibriert. Es gibt eine Reihe von verschiedenen Kalibrierverfahren, wobei in dieser Übung mit Hilfe eines Schachbrettmusters gearbeitet wird. Das Ergebnis eines solchen Prozesses ist eine Kameramatrix, welche genau die einzigartige Verzerrung und Störung der verwendeten Kamera beschreibt. Somit ist es dann möglich, exakte Distanzen auch mit nur einer Kamera zu messen. Theoretisch ist mit dem Puzzlebot auch eine Stereokalibrierung möglich, da dieser zwei festmontierte Kameras besitzt. Aufgrund der Komplexität der Kalibrierung von zwei Kameras wird in diesem Onlinelabor nur eine Kamera verwendet.

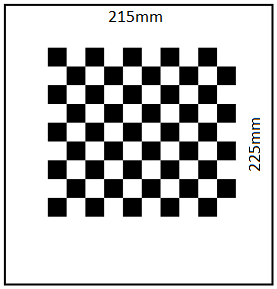
Bei einer Kamerakalibrierung gibt es einige Schritte, welche notwendig sind, um ein entstörtes kalibriertes Bild zu erhalten. Für die Kalibrierung wird ein Schachbrettmuster verwendet, welches zuerst aus verschiedenen Positionen und Orientierungen mit der Kamera fotografiert werden muss. In der folgenden Abbildung wird ein eigens für den Puzzlebot kreiertes Schachbrett mit Arbeitsbereich gezeigt. Die Dimensionen des Kalibrierobjekts betragen:

• Breite des Arbeitsfelds: 215mm
• Höhe des Arbeitsfelds: 225mm
• Anzahl der Kacheln: 10x9
• Kachellänge: 15mm

Da der Puzzlebot im Normalbetrieb nur über fest montierte Kameras verfügt, werden verschiedene Fotos zur Verfügung gestellt. Diese können HIER heruntergeladen werden. Im ersten Schritt gilt es herauszufinden, welche der Fotos für eine Kalibrierung geeignet oder nicht geeignet sind. Nur Fotos mit ausreichender Belichtung, Schärfe und Kontrast sowie Fotos, welche überhaupt ein Schachbrettmuster der richtigen Dimension enthalten, sind zulässig. Mit der Funktion cv2.findChessboardCorners() kann jedes einzelne Bild auf ein Schachbrettmuster der richtigen Dimension überprüft werden. Wichtig ist hierbei, dass die Funktion nur mit Bildern in Graustufen arbeiten kann. Weiters ist zu erwähnen, dass alle zu überprüfenden Bilder die gleiche Auflösung, das bedeutet auch von der gleichen Kamera, mit denselben Einstellungen stammen sollten. Ist dies nicht der Fall, so wird die Funktion cv2.findChessboardCorners() nicht korrekt ausgeführt. Es ist unbedingt erforderlich, vorher die Bilder auf deren Auflösung zu prüfen. Mit den Funktionen image.get(cv2.CAP_PROP_FRAME_WIDTH) und image.get(cv2.CAP_PROP_FRAME_HEIGHT) ist es möglich die Breite und Höhe jedes eingelesenen Bildes auszulesen. Somit kann jeder Wert abgespeichert und mit Werten anderer Bilder verglichen werden.

Sobald im ersten Schritt Kanten des Schachbretts in einem Bild erkannt wurden, müssen diese in einer Variable abgespeichert werden. Zusätzlich müssen sogenannte Bild- und Objektpunkte definiert werden. Die Bildpunkte (engl.: image-points) geben den Pixelwert der gefundenen Kante des Schachbretts im jeweiligen Bild an. Wenn ein Bild in Python geladen wird, dann liegt dieses als Matrix vor. Die Anzahl der vertikalen Matrix-Einträge entspricht der Höhe des Bildes in Pixel, die Anzahl der Horizontalen der Breite. Somit kann bestimmt werden, wo genau auf dem Bild sich eine Kante des Schachbretts befindet. Die Objektpunkte hingegen beschreiben, wo sich die Kante des Schachbretts in einem dreidimensionalen Koordinatensystem in der Realität befindet. So kann beispielsweise festgelegt werden, welchen Abstand die Kanten zueinander und welche Größe die Kacheln des Schachbretts haben. Somit ist es dann auch weiterführend möglich, die Position von Gegenständen im Raum zu bestimmen.

Sind die Bild- und Objektpunkte deklariert so müssen anschließend zu jedem Bild, in welchem Kanten erkannt wurden auch diese Punkte zugeordnet werden. Der spätere Kalibrierungsprozess ist nur erfolgreich, wenn genügend Bilder mit Bild- und Objektpunkten versehen wurden. Für eine Kalibrierung sollten mindestens zehn valide Bilder verwendet werden. In der Theorie funktioniert eine Kamerakalibrierung mit nur zwei, aus unterschiedlichen Winkeln aufgenommenen, Bildern. Je mehr Bilder allerdings verwendet werden, desto besser funktioniert der Prozess.

Mit der Funktion cv2.cornerSubPix() werden die bestimmten Kanten des Schachbretts in jedem einzelnen Bild noch verfeinert. Diese verbesserte Darstellung der wirklichen Eckpunkte eines Feldes im Schachbrett ist notwendig, um die Genauigkeit der nachfolgenden Kalibrierung zu gewährleisten. Mit den verfeinerten Kanten können nun auch zur Veranschaulichung die einzelnen Punkte grafisch ausgegeben werden.

Der letzte Schritt ist die eigentliche Kamerakalibrierung. Von der Funktion cv2.calibrateCamera() wird schlussendlich eine Kameramatrix und ein Verzerrungskoeffizient zurückgegeben. Diese sollten unbedingt in einer Datei abgespeichert werden, um sie bei den weiteren Übungen wiedereinzusetzen und genaue Ergebnisse zu erhalten.

Um Objekte tatsächlich mit dem Puzzlebot bewegen zu können, müssen diese vorher erkannt werden. Es gibt einige Methoden, um geschlossene Objekte zu detektieren. In der zweiten Übung wird mit einer sogenannten Hough Transformation gearbeitet. Diese kann für eine Kreis- und Linienerkennung verwendet werden. Das Ziel der Übung ist das Erfassen von Münzen und anderen eisenhaltigen Objekten im Arbeitsbereich des Puzzlebots.

Zu Beginn dieser Aufgabe muss ein Bild in das Programm geladen werden. Im ersten Schritt der zweiten Aufgabe sollen Kreise erkannt werden. Diese werden mittels Hough Transformation detektiert. Die Hough Transformation wird zum Erkennen geometrisch bekannter Formen verwendet. Dazu werden Bilder in den Hough-Raum transformiert. Jeder Punkt, der auf einer Kante (Gerade) liegen könnte, wird zunächst als Schnittpunkt von unendlich vielen Geraden bezeichnet. Im Hough-Raum ist dann für Punkte welche auf einer gemeinsamen Geraden liegen eine Häufung zu sehen. Diese Häufung beschreibt eine Gerade oder Kante im echten Bild. Zu beachten ist, dass der Hough Algorithmus nur mit Bildern in Graustufen arbeiten kann. Um Kreise vernünftig erkennen zu können, ist es notwendig das Bild mit einem Blur Filter zu verändern. Dieser Filter sorgt dafür, dass Kanten des Bildes weichgezeichnet werden und nur Kreise erkannt werden, welche auch wirklich Kreise sind. Mit der Funktion cv2.medianBlur() kann eine solche Wirkung erzielt werden. In der folgenden Abbildung ist ein Symbolfoto zu sehen welches diese Funktion deutlich macht. Es ist anschaulich zu erkennen, dass die Kanten des Symbolbildes weichgezeichnet wurden.

Im nächsten Schritt können mit Hilfe der in OpenCV enthaltenen Funktion cv2.HoughCircles() Kreise detektiert und diese in einer Variable abgespeichert werden. Wichtig ist hier zu beachten, dass die Funktion cv2.HoughCircles() nur die Position und Dimension der Kreise angibt falls diese auch gefunden wurden. Befindet sich kein Kreis in dem Bild, so gibt die Funktion nichts zurück. Für eine weitere Bearbeitung muss der Fall berücksichtigt werden. Im Folgenden muss schließlich der Mittelpunkt der Kreise ausgelesen werden. Zunächst werden die Werte in der Variable des gefundenen Kreises gerundet. Danach kann der Mittelpunkt mit X und Y Koordinate und der Radius R aus der Variable entnommen werden. Der Mittelpunkt eines Kreises ist auch gleichzeitig sein Schwerpunkt. Für eine Münze mit gleichbleibender Dichte beispielsweise, ist der Schwerpunkt also der optimale Punkt, um von einem Roboter manipuliert zu werden. Die Funktion cv2.circle() ist hilfreich, wenn die gefundenen Kreise auch grafisch im Bild hinterlegt werden sollen.

Die Erkennung der magnetischen Puzzleteile funktioniert auf andere Art und Weise. In der nachfolgenden Abbildung ist der Arbeitsraum des Puzzlebots zu sehen. Die Abbildung wurde mit der Kamera, welche an dem Roboter befestigt ist, aufgenommen. Des Weiteren sind die erkannten Puzzleteile mit ihrem Schwerpunkt durch Umrandungen markiert.

Die Puzzleteile werden anhand ihrer ganz speziellen Farbe erkannt. Dazu muss das gesamte Bild zunächst in den HSV-Farbraum konvertiert werden. Mit der Funktion cv2.cvtColor() und dem Parameter cv2.COLOR_BGR2HSV wird das Bild konvertiert und kann dann weiterbearbeitet werden. Zunächst muss mit Hilfe einer Maske und einem oberen und unteren Grenzwert definiert werden, welchen Farbwert, welche Farbsättigung und welcher Hellwert gesucht wird. Danach kann mit der Funktion cv2.inRange() die Maske über das Bild gelegt werden, und es sind nur mehr die markanten grün bis ockerfarbenen Stellen der Puzzleteile zu sehen. Nun können mit der Funktion cv2.findContours() die Konturen der Teile gefunden und mit der Funktion cv2.approxPolyDP() diese auch als geschlossene Konturen erkannt werden. Es ist hilfreich, die Funktion cv2.drawContours() zu verwenden, um die erkannten Konturen am Originalbild zu visualisieren. Der Schwerpunkt kann mit der Funktion cv2.moments() gefunden werden, um die Puzzleteile in den nachfolgenden Übungen auch vernünftig handhaben zu können.

Die Kamerakalibrierung hat zwar den grundsätzlichen Zweck einer Entstörung des Bildes, jedoch werden hier auch automatisch die festgestellten Kanten zwischen den einzelnen Kacheln als Objektpunkte gespeichert. Genau diese Daten können nun genutzt werden, um den Abstand zwischen den einzelnen Kacheln festzulegen. Der Abstand ist bei einem symmetrischen Schachbrett immer gleich, somit ist es möglich den Abstand von und zu allen Bildpunkten zu bestimmen. Im Folgenden kann also der Schwerpunkt einer Münze oder eines anderen Objektes, in Bezug auf einen vorher festgelegten Koordinatenursprung, exakt bemessen werden. Es wird also eine Distanz beziehungsweise Länge vom Schwerpunkt zum Ursprung erhalten. Danach kann auch noch der Winkel dieser Linie zur X-Achse bestimmt werden. Somit errechnen sich daraus die Polarkoordinaten des Ziels. Im letzten Schritt werden die Polarkoordinaten in kartesische Koordinaten umgewandelt und in das Roboterkoordinatensystem überführt. Nun kann der Puzzlebot die X und Y Koordinaten des Objekts genau anfahren und diese hochheben oder absenken.

Für die dritte Aufgabe empfiehlt es sich, die vorherigen Aufgaben in Funktionen zu implementieren. Das in den ersten beiden Übungen erworbene Wissen, wird hier wieder benötigt. Die Herangehensweise für die Übung 3 in dieser Erklärung, stellt nur eine von mehreren Möglichkeiten dar, diese Aufgabe zu lösen. Nach erfolgreicher Kalibrierung der Kamera und Detektion der Objekte im Arbeitsraum muss ein Referenzpunkt (Ursprung) des Koordinatensystems festgelegt werden. Mit der Funktion cv2.cornerHarris() ist es möglich Ecken zu finden. Da das Kamerabild üblicherweise nicht nur die Ecke enthält, welche benötigt wird, ist es erforderlich, den mit der Funktion zu untersuchenden Bereich dahingehend einzugrenzen. In der nachfolgenden Abbildung ist der Arbeitsraum des Puzzlebots zu sehen. Dieses Bild wurde mit der am Puzzlebot befestigten Kamera aufgenommen. Die rechte obere Ecke des Arbeitsraums wurde erkannt, und zur besseren Veranschaulichung mit zwei Linien markiert. Diese Linien stellen hier die X-Achse und die Y-Achse dar und werden mit der Funktion cv2.line() in ein Bild gezeichnet. Die Ecke ist also der Ursprung des Koordinatensystems.

Nun kann der Abstand zwischen den Objekten und dem Ursprung mathematisch sehr einfach errechnet werden. Die folgende Formel berechnet den Abstand zwischen Ursprung und Objekt.

$$d² = (y₂ - y₁)² + (x₂ - x₁)²

Wobei hier (x₁=y₁) den Ursprung und (x₂=y₂) das erkannte Objekt beziehungsweise das Ziel darstellt. Eine weitere Möglichkeit besteht darin die X- und Y-Koordinaten einfach von einander zu subtrahieren und den Betrag des Ergebnisses als jeweilige Änderung der Koordinaten zu sehen. Die Änderung ist in folgender Formel zu sehen.

$$δx = |x₁ - x₂|
δy = |y₁ - y₂|

Diese Änderung bezieht sich nun auf die Pixel des jeweiligen Bildes und muss noch in das Roboter-Koordinatensystem überführt werden. Da sich die Kamera am Roboter auch minimal ungewollt bewegen kann ist es erforderlich, die Überführung in das Roboterkoordinatensystem bei jeder Verwendung erneut durchzuführen. Eine Möglichkeit dies zu tun ist ein Verhältnis aufzustellen. Dieses Verhältnis kommt zustande, da einige Abmessungen, wie zum Beispiel das Schachbrett, bekannt sind. Wichtig ist hierbei, dass unbedingt ein kalibriertes Bild verwendet werden muss. In der nachfolgenden Formel ist ein Beispiel einer solchen Rechnung zu sehen. Die linke Seite der Rechnung stellt die bekannte Länge in Millimeter gebrochen durch die gemessenen Pixel der bekannten Länge dar. Der Bruch auf der rechten Seite zeigt die unbekannte Länge in Millimeter durch die gemessenen Pixel zum Objekt. Durch eine Referenzlänge kann somit jede benötigte Distanz über dieses Verhältnis errechnet werden. Wichtig hierbei ist auch, dass die Rechnung sowohl für die X-Koordinate als auch für die Y-Koordinate separat durchgeführt werden muss.

Danach ist es möglich den Roboter aus dem Koordinatenursprung zielgerichtet zu einem Objekt zu steuern.

Die Steuerung des Puzzlebots erfolgt von außen nur durch einen OPC UA Server, welcher die Befehle an einen Arduino Mega weiterleitet, um den Roboter mittels G-Code anzusteuern. Da für diese Übungen nur eine OPC UA Verbindung zur Verfügung steht, wird ein OPC UA Client benötigt. Dieser Client muss verschiedene Knoten, sowie deren Werte vom Server auslesen und beschreiben können. Dies geschieht über Methoden, welche am Server implementiert sind. Jeder Wert besitzt eine eindeutige Identifikationsnummer, mit welcher dieser Wert ausgelesen und beschrieben werden kann. Für die folgende Programmierung wird auf die OPC UA Bibliothek von Python zurückgegriffen.

Als ersten Schritt für die vierte Übung empfiehlt es sich, den OPC UA Server des Puzzlebots etwas genauer zu betrachten. Hierzu wird am besten das Programm UA Expert von Unified Automation verwendet. Dabei handelt es sich um einen OPC UA Client, welcher das Durchsuchen des Namensraumes unterstützt und alle Knoten (engl.: node) und Methoden übersichtlich darstellt. Es ist auch möglich einen Live-Video Stream der Kamera des Puzzlebots abzurufen.

Zum eigentlichen Lesen und Schreiben von Werten muss zu Beginn eine Verbindung zum Server aufgebaut werden. Diese Verbindung wird mit Hilfe eines Benutzernamens und eines Passworts authentifiziert. Für die Anmeldung am Server werden in einem Python Script die Funktionen Client() und connect() verwendet. In der Funktion Client() werden Benutzername, Passwort, Hostname sowie Port übergeben, um mit der Funktion connect() die Verbindung herzustellen. Danach kann mit der Funktion get_namespace_index() der Namensraum des Puzzlebots ausgewählt werden, um anschließend auf die Knoten zugreifen zu können. Mit der Funktion get_node() ist unter Angabe des Namensraums und der Kennung (engl.: identifier) des entsprechenden Knotens ein Zugriff möglich. Mit der Funktion get_value() ist ein Lesen des im Knoten beinhalteten Wertes möglich. Falls es der OPC UA Server erlaubt können auch Werte eines Knotens direkt mit set_value() geschrieben werden. Normalerweise und um zu gewährleisten, dass nicht unzulässige Werte in einen Knoten geschrieben werden, wird der Schreibvorgang über eine Methode erledigt und sind Werte nicht direkt beschreibbar. Über eine Methode kann der Wert, welcher verändert werden soll, überprüft und bei Unzulässigkeit verworfen werden. Als Beispiel kann eine Verfahrensachse des Puzzlebots gezeigt werden. Die X-Achse kann beispielsweise für Werte zwischen 5 und 210 bewegt werden. Andernfalls würde ein Schaden an den Motoren des Puzzlebots auftreten. Wird die Achse nun mit einem Wert unter 5 oder über 210 beschrieben, verwirft die Methode, welche für die Achsensteuerung verantwortlich ist, diesen Wert und gibt eine Fehlermeldung zurück.

Um schließlich eine Methode aufrufen zu können, wird die Funktion call_method() verwendet. Mit dieser Funktion lassen sich sowohl Werte aus der Methode lesen, als auch in diese schreiben, um so schlussendlich den Roboter anzusteuern. Als letzten Schritt ist es unbedingt erforderlich, mit der Funktion disconnect() die Verbindung zum Server wieder zu schließen. Manche OPC UA Server verneinen das Eingehen von mehreren parallelen Verbindungen um Konflikte zu vermeiden. Ist die Verbindung nicht ordnungsgemäß beendet worden, muss diese am Server manuell beendet werden.

Eine detaillierte Übungsbeschreibung im PDF-Format zur Durchführung der Kamerakalibrierung kann HIER heruntergeladen werden. Die notwendigen Bilder für die Kamerakalibrierung können HIER heruntergeladen werden.

Eine detaillierte Übungsbeschreibung im PDF-Format zur Durchführung der Übung kann HIER heruntergeladen werden.

Eine detaillierte Übungsbeschreibung im PDF-Format zur Durchführung der Übung kann HIER heruntergeladen werden.

Eine detaillierte Übungsbeschreibung im PDF-Format zur Durchführung der Übung kann HIER heruntergeladen werden.

Mit dieser Funktion werden Bilder hinsichtlich eines Schachbrettmusters mit bestimmter Dimension überprüft. Dadurch kann festgestellt werden, ob sich die Bilder für eine Kamerakalibrierung eignen.

Sie ermöglicht es, bekannte Geometrien wie z.B. Kreise in Bildern zu erkennen. Die OpenCV Python Bibliothek enhtält bereits Funktionen, um bestimmte Geometrien zu identifizieren. Beispielsweise wird für die Erkennung von Kreisen die Funktion cv2.HoughCircles verwendet.

Die Umrechnung wird über das Längen/Pixelvehältnis durchgeführt. Dazu dient ein kalibriertes Bild mit bekannten Abmessungen - wie beispielsweise die Kacheln des Schachbrettmusters. Durch eine einfache Schlussrechnung kann dadurch eine unbekannte Länge aber bekannter Pixelanzahl berechnet werden.

Über Methoden kann der zu schreibende Wert auf Gültigkeit überprüft werden, was beim direkten Schreiben nicht möglich ist. Deshalb wird das direkte Schreiben üblicherweise nicht erlaubt.