• OPC UA Python library
• OpenCV Python library
• Pillow Python library (with Image Modul)

In order to get access to this online laboratory, following information are required:

• Namespace URI: opc.tcp://engine.ie.technikum-wien.at/PuzzleBot
• Root node of the puzzlebot: ns=1;s=Puzzlebot
• username: puzzlebot

The communication basics are explained HERE. Note, that an interaction with the hardware is only possible with the usage of the communication protocol OPC UA.

Every camera has a certain amount of distortion and interference. This is due to the curvature of the lens and the construction of a camera. For exact measuring of lengths or for the exact determination of a position in the camera image it is therefore important to calibrate the camera first. In this step the camera is suppressed and calibrated to a defined pattern. There are a number of different calibration procedures, but in this exercise you will work with a checkerboard pattern. The result of such a process is a camera matrix that describes exactly the unique distortion and interference of the camera used. Thus it is then possible to measure exact distances even with only one camera. Theoretically, stereo calibration is also possible with the Puzzlebot, as it has two fixed cameras. Due to the complexity of calibrating two cameras, only one camera is used in this online laboratory.

There are several steps in a camera calibration that are necessary to get a calibrated image that is free of interference. For the calibration a checkerboard pattern is used, which first has to be photographed with the camera from different positions and orientations. The following figure shows a chessboard with a working area, which was created especially for the Puzzlebot. The dimensions of the calibration object are as follows:

• width of the workspace: 215mm
• height of the workspace: 225mm
• number of chessboard squares: 10x9
• length of chessboard square: 15mm

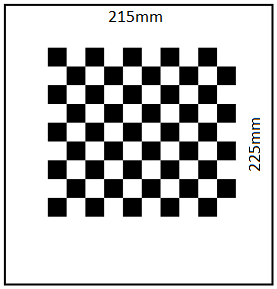
Since the Puzzlebot only has fixed cameras in normal operation, various photos are provided. These can be downloaded HIER. The first step is to find out which of the photos are suitable or unsuitable for calibration. Only photos with sufficient exposure, sharpness and contrast, as well as photos that contain a checkerboard pattern of the correct dimension at all, are allowed. With the function cv2.findChessboardCorners() every single photo can be checked for a checkerboard pattern of the correct dimension. It is important that the function can only work with images in grayscale. It should also be mentioned that all images to be checked should have the same resolution, i.e. also from the same camera, with the same settings. If this is not the case, the function cv2.findChessboardCorners() is not executed correctly. It is absolutely necessary to check the images for their resolution before. With the functions image.get(cv2.CAP_PROP_FRAME_WIDTH) and image.get(cv2.CAP_PROP_FRAME_HEIGHT) it is possible to read out the width and height of each scanned image. So every value can be stored and compared with values of other images.

As soon as in the first step edges of the chessboard have been recognized in an image, they must be stored in a variable. In addition so-called image and object points must be defined. The image-points indicate the pixel value of the found edge of the chessboard in the respective image. When an image is loaded into Python, it is available as a matrix. The number of vertical matrix entries corresponds to the height of the image in pixels, the number of horizontal entries to the width. This allows to determine where exactly on the image an edge of the chessboard is located. The object points, on the other hand, describe where the edge of the chessboard is located in a three-dimensional coordinate system in reality. For example, it is possible to determine the distance between the edges and the size of the chessboard tiles. This makes it possible to further determine the position of objects in space.

Once the image and object points have been declared, these points must be assigned to each image in which edges were detected. The later calibration process is only successful if enough images have been provided with image and object points. For a calibration at least ten valid images should be used. In theory, a camera calibration works with only two images taken from different angles. However, the more images are used, the better the process works.

The function cv2.cornerSubPix() refines the specific edges of the chessboard in each individual image. This improved representation of the real corners of a field in the chessboard is necessary to ensure the accuracy of the subsequent calibration. With the refined edges, the individual points can now also be output graphically for illustration purposes.

The last step is the actual camera calibration. The function cv2.calibrateCamera() finally returns a camera matrix and a distortion coefficient. These should definitely be saved in a file to be able to use them again in further exercises and to get exact results.

In order to actually move objects with the Puzzlebot, they have to be recognized before. There are several methods to detect closed objects. In this exercise you will work with a so-called Hough Transformation. This can be used for circle and line detection. The goal of the exercise is to detect coins and other ferrous objects in the working area of the puzzlebot.

At the beginning of this task an image must be loaded into the program. In the first step of this task, circles are to be detected. These are detected by means of Hough Transformation. The Hough Transformation is used to detect geometrically known shapes. Therefore images are transformed into the Hough space. Every point that could lie on an edge (straight line) is first called the intersection of infinitely many straight lines. In the Hough space, points lying on a common straight line are then clustered. This accumulation describes a line or edge in the real image. Note that the Hough algorithm can only work with images in grayscale. To be able to detect circles properly, it is necessary to modify the image with a blur filter. This filter ensures that edges of the image are blurred and only circles that are actually circles are recognized. With the function cv2.medianBlur() such an effect can be achieved. In the following figure you can see a symbol photo which makes this function clear. It can be clearly seen that the edges of the symbol image have been blurred.

In the next step, circles can be detected and stored in a variable using the function cv2.HoughCircles() contained in OpenCV. It is important to note that the function cv2.HoughCircles() only gives the position and dimension of the circles if they were found. If there is no circle in the image, the function returns nothing. For further processing the case must be considered. In the following the center of the circles must be read. First the values in the variable of the found circle are rounded. Then the center point with X and Y coordinates and the radius R can be taken from the variable. The center of a circle is also its center of gravity. For a coin with a constant density, for example, the center of gravity is therefore the optimal point to be manipulated by a robot. The function cv2.circle() is helpful, if the found circles should also be stored graphically in the image.

The recognition of the magnetic puzzle pieces works in a different way. The following figure shows the working space of the puzzle bot. The picture was taken with the camera attached to the robot. Furthermore, the recognized puzzle pieces are marked with their center of gravity by borders.

The puzzle pieces are recognized by their very special color. To do this, the entire image must first be converted to the HSV color space. With the function cv2.cvtColor() and the parameter cv2.COLOR_BGR2HSV the image is converted and can then be processed further. First, with the help of a mask and an upper and lower limit value, it must be defined which color value, color saturation, and lightness value is sought. Afterwards, the mask can be placed over the image with the function cv2.inRange() and only the prominent green to ochre parts of the puzzle pieces are visible. Now the function cv2.findContours() can be used to find the contours of the pieces, and the function cv2.approxPolyDP() can be used to recognize these as closed contours. It is helpful to use the function cv2.drawContours() to visualize the recognized contours on the original image. The center of gravity can be found with the function cv2.moments() in order to be able to handle the puzzle pieces reasonably in the following exercises.

Although the camera calibration has the basic purpose of removing interference from the image, the detected edges between the individual tiles are also automatically saved as object points. Exactly this data can now be used to determine the distance between the individual tiles. The distance is always the same for a symmetrical chessboard, so it is possible to determine the distance from and to all pixels. So in the following the center of gravity of a coin or other object can be measured exactly, in relation to a previously defined coordinate origin. Thus a distance or length from the center of gravity to the origin is obtained. Afterwards, the angle of this line to the X-axis can also be determined. Thus the polar coordinates of the target are calculated. In the last step the polar coordinates are converted into cartesian coordinates and transferred to the robot coordinate system. Now the Puzzlebot can precisely approach the X and Y coordinates of the object and raise or lower them.

For the third task it is recommended to implement the previous tasks in functions. The knowledge acquired in the first two exercises is needed here again. The approach for exercise 3 in this explanation is only one of several ways to solve this task. After successful calibration of the camera and detection of the objects in the working space, a reference point (origin) of the coordinate system must be defined. With the function cv2.cornerHarris() it is possible to find corners. Since the camera image usually does not only contain the corner that is needed, it is necessary to limit the area to be examined with the function. The following figure shows the workspace of the puzzle bot. This image was taken with the camera attached to the Puzzlebot. The upper right corner of the workspace was detected and marked with two lines for better visualization. These lines represent here the X-axis and the Y-axis and are drawn into an image with the function cv2.line(). The corner is thus the origin of the coordinate system.

Now the distance between the objects and the origin can be calculated mathematically very easily. The following formula calculates the distance between origin and object.

$$d² = (y₂ - y₁)² + (x₂ - x₁)²

Here (x₁=y₁) represents the origin and (x₂=y₂) the recognized object and the target respectively. Another possibility is to subtract the X- and Y-coordinates from each other and to see the amount of the result as a respective change of the coordinates. The change can be seen in the following formula.

$$δx = |x₁ - x₂|
δy = |y₁ - y₂|

This change now refers to the pixels of the respective image and must still be transferred to the robot coordinate system. Since the camera on the robot can move even minimally unintentionally, it is necessary to transfer the image into the robot coordinate system again each time it is used. One way to do this is to set up a relationship. This ratio is created because some dimensions, such as the chessboard, are known. It is important that a calibrated image is used. The following formula shows an example of such a calculation. The left side of the calculation represents the known length in millimeters broken by the measured pixels of the known length. The fraction on the right side shows the unknown length in millimeters through the measured pixels to the object. By using a reference length, any required distance can be calculated using this ratio. It is also important to note that the calculation must be performed separately for both the X-coordinate and the Y-coordinate.

Then it is possible to steer the robot from the coordinate origin to an object.

The puzzlebot is controlled from the outside by an OPC UA server, which forwards the commands to an Arduino Mega to control the robot using G-code. Since only an OPC UA connection is available for these exercises, an OPC UA client is required. This client must be able to read and write to different nodes and their values from the server. This is done using methods that are implemented on the server. Each value has a unique identification number with which this value can be read and written. For the following programming the OPC UA library of Python is used.

As a first step it is recommended to take a closer look at the OPC UA server of the puzzle bot. The best way to do this is to use the program UA Expert from Unified Automation. This is an OPC UA client that supports searching the namespace and clearly displays all nodes and methods. It is also possible to get a live video stream from the puzzlebot's camera.

For the actual reading and writing of values a connection to the server must be established at the beginning. This connection is authenticated with a user name and password. To log on to the server, the functions Client() and connect() are used in a Python script. In the function Client() username, password, hostname and port are passed to establish the connection with the function connect(). Afterwards the namespace of the puzzlebot can be selected with the function get_namespace_index() to access the nodes afterwards. The function get_node() can be used to access the nodes by specifying the namespace and the identifier of the corresponding node. With the function get_value() it is possible to read the value contained in the node. If the OPC UA Server allows it, values of a node can also be written directly with set_value(). Normally and to ensure that not invalid values are written to a node, the write operation is done by a method and values are not directly writable. A method can be used to check the value to be changed and discarded if it is invalid. As an example a method axis of the puzzlebot can be shown. The X-axis can be moved for values between 5 and 210. Otherwise the motors of the puzzlebot would be damaged. If the axis is now described with a value below 5 or above 210, the method responsible for axis control discards this value and returns an error message.

To finally call a method, the function call_method() is used. This function can be used to read values from the method as well as to write them into the method to finally control the robot. The last step is to close the connection to the server with the function disconnect(). Some OPC UA servers deny multiple parallel connections to avoid conflicts. If the connection has not been closed properly, it must be closed manually on the server.

A detailed exercise description in PDF format for performing the camera calibration can be downloaded HERE. The necessary images for the camera calibration can be downloaded HERE.

A detailed exercise description in PDF format for performing the exercise can be downloaded HERE.

A detailed exercise description in PDF format for performing the exercise can be downloaded HERE.

A detailed exercise description in PDF format for performing the exercise can be downloaded HERE.

With this function images are checked for a checkerboard pattern with a certain dimension. This way it can be determined whether the images are suitable for camera calibration.

It allows to recognize known geometries such as circles in images. The OpenCV Python library already contains functions to identify certain geometries. For example, the function cv2.HoughCircles is used to recognize circles.

The conversion is done via the length/pixel ratio. Therefore a calibrated image with known dimensions is used - such as the tiles of the checkerboard pattern. By a simple final calculation an unknown length but known number of pixels can be calculated.

Using methods, the value to be written can be checked for validity, which is not possible with direct writing. Therefore direct writing is usually not allowed.